Logaritmické pravítko ve 21. století:
Vzkříšení historické výpočetní pomůcky

Oliver Steffens, 25. 8. 2020

Mají smysl nová logaritmická pravítka v době umělé inteligence a velkých dat? Ano! Pravítko – jako mechanický předchůdce dnešního počítače či kalkulačky a zároveň názorná pomůcka sloužící k pochopení základních matematických vztahů – dokáže i dnes být hascinujícím a zároveň velmi praktickým pomocníkem ve výuce i praxi. V tomto článku podávám zprávu o vývoji aa výrobě svých vlastních kruhových logaritmických pravítek. Co mě k tomu vede? V první řadě je to samozřejmě nadšení pro tyto mechanické „analogové počítače“, zejména jejich použití v haptice a při vizualizaci zajímavých problémů. Kromě toho se nabízí zajímavá otázka: daly by se osvědčené principy a zkušenosti z dlouhé historie logaritmických pravítek obohatit o nové nápady? Jaká praktická a zároveň estetická řešení se nabízí?

Po orientačním historickém přehledu představím několik nových logaritmických pravítek své vlastní konstrukce a stručně popíšu, jak se vyrábějí v praxi.

1. Nástin historie logaritmického pravítka

Použití mechanických počítacích pomůcek, jako jsou logaritmická pravítka, má v historii matematiky a techniky dlouhou tradici.

Klasické posuvné logaritmické pravítko je založené na myšlence, že problém násobení či dělení lze při vhodně navržené stupnici převést na mnohem jednodušší problém sčítání a odčítání délek. Takové pravítko vzniklo záhy po původním objevu logaritmů Skotem Johnem Napierem (1550–1617). Napier se v latinských textech uváděl jako Neper a v této formě se jeho jméno dodnes používá jako fyzikální jednotka pro přirozený logaritmus poměru dvou hodnot. Napier svou metodu publikoval v roce 1614 v díle „Mirifici logarithmorum canonis descriptio ejusque usus in utraque trigonometria ; ut etiam in omni logistica mathematica, Amplissimi, facillimi, & expeditissimi explicatio“ [1] , tj. „Popis podivuhodného principu logaritmů a jejich použití nejen v trigonometrii, ale i ve všech matematických výpočtech, plně a co nejjednodušeji vysvětlený“. Pomocí logaritmů se lze, podle jeho vlastních slov, vyhnout „velkému zdržení způsobenému zdlouhavým násobením a dělením, výpočtem poměrů nebo odmocnin“ a také „nepříjemnostem způsobeným mnoha chybami z nepozornosti“. Napierovy poznatky převzal a dále rozvinul jeho současník Henry Briggs (1556–1630). [2]

Téměř současně zavedl logaritmy Švýcar Jost Bürgi (1552–1632). Byl císařským dvorním hodinářem a konstruktérem prvních astronomických hodin s vteřinovkou. Konstruoval též přesné nebeských glóby a nejrůznější vědecké měřicí přístroje a navrhl možnosti využití diskrétního počtu v astronomii jakož i mnohé unikátní výpočetní postupy. [3] V roce 1620 sestavil a vydal první logaritmické tabulky na světě: „Aritmetische und Geometrische Progress Tabulen“. [4]

Roku 1620 Angličan Edmund Gunter (1581–1626) poprvé vynesl Napierův logaritmus na stupnici. Takto vzniklá Gunterova stupnice (Gunter’s Line), vyznačená na dřevěné tyči o délce dvou stop, již sloužila k provádění základních výpočtů s pomocí odpichovátka, resp. kružítka. Později byla doplněna o trigonometrickou a balistickou stupnici a v této podobě se dlouho, až do počátku 20. století, používala jako výpočetní pomůcka v námořní navigaci. [5] Gunter také zavedl pojmy ko-sinus a ko-tangens. [6]

Z této někdejší podoby se vyvinulo dnes známé posuvné logaritmické pravítko, které se skládá ze dvou logaritmických stupnic, jež se mohou proti sobě posouvat, a k měření tak již není třeba odpichovátko. Tento vynález pochází z roku 1622 a je dílem anglického matematika Williama Oughtreda (1574–1660). Oughtred byl duchovním anglikánské církve a jako soukromý učitel vyučoval matematice. Jeho žákem byl, mezi jinými, Christopher Wren (1632–1723), slavný astronom a zakladatel Královské společnosti. Oughtred byl považován za předního matematika své doby. Mimochodem, od něj pochází např. použití symbolu π pro obvod kruhu (jako „Peripherie“ – obvod) nebo operátorů × a  ∕  pro násobení a dělení. [7]

V roce 1632 Oughtred zveřejnil svůj nápad na kruhové logaritmické počítadlo. V knize „Circles of Proportion“ [8] uvádí:

„That the true way of Art is not by Instruments, but by Demonstration: and that it is a preposterous course of vulgar Teachers, to begin with Instruments, and not with the Sciences, and so instead of Artists, to make their Scholars only doers of tricks, and as it were jugglers: to the despite of Art, loss of previous time, and betraying of willing and industrious wits, unto ignorance, and idleness. That the use of Instruments is indeed excellent, if a man be an Artist: but contemptible, being set and opposed to Art.“ [9]

Na tomto místě mluví Oughtred z duše přátelům a sběratelům logaritmických pravítek. Vždyť matematické principy lze znázornit mnohem lépe graficky než na kalkulačce. Jako by Oughtred předvídal budoucí vývoj; zavedení elektronické kalkulačky (navzdory všem jejím praktickým výhodám) vedlo k tomu, že samotné podstatě výpočtu rozumíme stále méně.

Historicky je však tento Oughtredův citát součástí jeho sporu s Richardem Delamainem (1600–1644). Ten podle zpráv některých současníků vydával mnohé Oughtredovy myšlenky za vlastní a předběhl Oughtreda s vydáním díla „Grammelogia“ [10] z roku 1630. [11] Kromě podrobného popisu kruhového logaritmického pravítka obsahuje tato kniha též první skutečný návod k použití posuvného pravítka. [12] Delamainův „matematický kruh“ neboli Grammelogia se skládal z jednoho pevného a jednoho pohyblivého kotouče, obou s logaritmickými stupnicemi. V Oughtredově knize „Circles of Proportion“ jsou kotouče pevné a vzdálenosti se měří podobně jako u Gunterovy stupnice. V pozdějším vydání „Grammelogie“ kolem roku 1632 popisuje Delamain fungování ukazatele čili běhounu, pročež se považuje za jeho vynálezce ještě před Isaacem Newtonem (1643–1727).

Oughtredův citát ukazuje, že matematiku a logiku chápal jako „umění“ (Art). Tím navazuje na dřívější úvahy katalánského filozofa a teologa Ramóna Llulla (Raimundus Lullus, 1232–1316). Po svém vlastním prozření si Llull vytkl za cíl přesvědčit nevěřící o pravdivosti křesťanské víry čistou logikou s pomocí logického aparátu, svého „Ars Magna“ („Velkého umění“). [13] Z dnešního pohledu to může vypadat podivně, ale v jeho době, kdy se křesťanství často prosazovalo za pomoci zbraní, byl jeho postoj pokrokový a nezvykle vstřícný. Zakládal si totiž na dialogu a diskusi a chtěl být racionálně přesvědčivý. Jako misionář se svým „Ars“ ovšem neuspěl a za svou misijní činnost nakonec zaplatil životem, když byl koncem roku 1315 kamenován davem v Tunisu. Těžce zraněn se vrátil na rodnou Mallorku, kde zemřel. Dnes je považován spíše za průkopníka kombinatoriky a informatiky, protože se zabýval základními otázkami datových struktur, algoritmů atd. [14]

Llullův počítací stroj „Ars Generalis Ultima“ (1305–1308) [15] sestává ze tří otočných kotoučů s písmeny. S pomocí takového „stroje na myšlení“ dokázal Llull prakticky realizovat svou „Ars Magna“, vyznačující se složitým systémem pravidel. Díky tomu jej lze považovat za významného předchůdce dnešních kruhových logaritmických pravítek.

2. Moderní pravítka: pocta historii i nové funkce

Mým cílem bylo vyjít z historických modelů logaritmických pravítek a na jejich základě vytvořit moderní varianty pro nové vědecké a technické disciplíny. Zároveň jsem chtěl vyzkoušet některé neotřelé myšlenky a nedržet se za každou cenu „zavedených“ metod.

V následujícím textu nejprve představím několik nových logaritmických i jiných výpočetních pravítek své konstrukce. Poté krátce vysvětlím postup, jímž jsem je vytvořil. Zvláštní pozornost věnuji postupu grafického zpracování, který mi umožňuje dodat každému z mých výrobků jedinečný vzhled.

a) Klasické kruhové pravítko

Typická kruhová logaritmická pravítka 70. let 20. století obvykle nabízela dvojice stupnic C a D o rozsahu jedné dekády, A a B (rozsah dvou dekád), někdy K (tři dekády), případně reciproké stupnice (CI a další). Velký význam mají často též trigonometrické funkce sinus, kosinus, tangens … O ně se Napier a jeho současníci obzvlášť zajímali. Pomocí logaritmické stupnice L, která je na logaritmickém pravítku vlastně lineární, se dají též počítat mocniny, i když poněkud nepohodlně. Posuďte sami:

Chcete-li vypočítat z = x^a, zjistíte nejprve s pomocí stupnice L hodnotu log(x) a potom násobením určíte log(z) = a · log(x). V tomto kroku se ovšem musíte přesunout na stupnice C a D, na nich provést násobení a potom se vrtátit zpět na stupnici L, kde přečtete, která hodnota z odpovídá zjištěnému log(z).

Celý postup se dá zjednodušit, máte-li ovšem k dispozici také exponenciální stupnici (LL). Ta je obvykle svázaná se stupnicí D, takže vyhledáte-li si na exponenciální stupnici hodnotu x, vidíte k ní na stupnici D odpovídající hodnotu ln(x), tj. přirozený logaritmus x. Ten stačí vynásobit exponentem a. Výsledek se pak znovu odečte ze stupnice LL proti takto zjištěnému násobku. Aby se výpočty tohoto druhu daly provádět v co největším rozsahu hodnot, nachází se na každém pravítku obvykle několik stupnic LL.

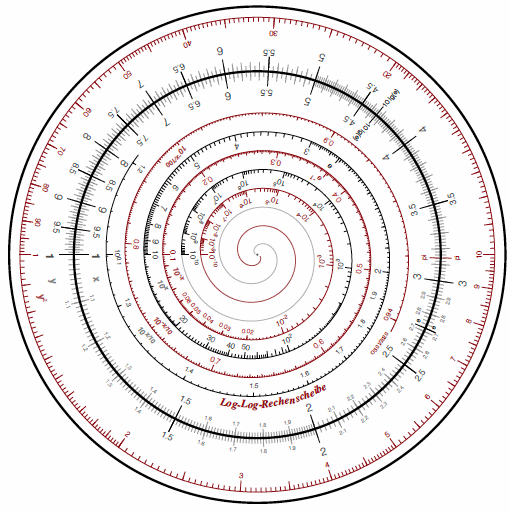
Obr. 1: Klasické kruhové logaritmické pravítko

Univerzální kruhové logaritmické pravítko obsahuje základní stupnice a běžné trigonometrické funkce. Celkem sestává z osmi stupnic na dvou kotoučích, které se dají proti sobě otáčet, a z běhounu s ryskou, která usnadňuje odečítání hodnot na různých stupnicích:

Na vnitřním kotouči (v pořadí od vnějšku ke středu) se nachází:

• Hlavní stupnice x (logaritmická), tzv. stupnice C
• Stupnice x² (logaritmická), tzv. stupnice B
• Přirozený logaritmus ln(x)
• Arcus tangens x a x/10, tzv. stupnice T

Na vnějším kotouči (v uspořádání od středu ven) se nachází:

• Hlavní stupnice y (logaritmická), tzv. stupnice D
• Exponenciální funkce e^y/10, tzv. stupnice LL2 s rozsahem od e^0,1 do e¹
• Exponenciální funkce e^y, tzv. stupnice LL3 s rozsahem od e¹ do e¹⁰
• Dekadický logaritmus log(y), tzv. stupnice L
• Arcus sinus y a y/10, tzv. stupnice S a ST

b) Kruhové pravítko se spirálovou stupnicí

Toto pravítko je inspirováno Fowlerovým pravítkem „Magnum Long-Scale Calculator“ (Manchester 1930, obr. 2). Na něm je stupnice D prodloužená a obsahuje několik dekád uspořádaných do soustředných kružnic, což vede k větší přesnosti při čtení.

Na rozdíl od Fowlera se na mém pravítku nenacházejí soustředné kružnice, ale stupnice D je vedena ve spirále (obr. 3), což zjednodušuje čtení a odstraňuje nutnost přeskakovat mezi kružnicemi.

Spirálové uspořádání stupnic známe např. z ruských kapesních pravítek КЛ-1 (Техническо-сбытовая организация “Рассвет”, 60. léta 20. století), ale tam se používá pouze pro funkci tangens.

Pravítko sestává pouze z jednoho pevného kotouče, proto má dva běhouny s ryskami, jejichž vzájemná vzdálenost, či svíraný úhel se dají odměřit.

Obr. 4: Unique Log Log Slide Rule (cca 1950)

Uspořádání stupnic vychází z modelu „Log Log Slide Rule“ (cca 1950, obr. 4) společnosti Unique Slide Rule Company, kterou založil Burns Snodgrass v Brightonu roku 1920, a která byla až do roku 1975 jedním z největších výrobců logaritmických pravítek ve Spojeném království. Burns Snodgrass (1896–1954) byl také autorem známé učebnice logaritmického pravítka pro samouky. [16]

Spirálovitě uspořádané stupnice jsou tři. Uprostřed je hlavní logaritmická stupnice x a po stranách exponenciální stupnice e^x/10 a e^x (viz Obr. 3). Ty umožňují výpočet mocnin s odchylkou menší než 0,5 %. Na vnějšku kotouče je také obyčejná logaritmická stupnice a různé další funkce (sinus, kosinus, tangens, kvadratická stupnice – viz Obr 5.). Podrobnější popis by si vyžádal více prostoru.

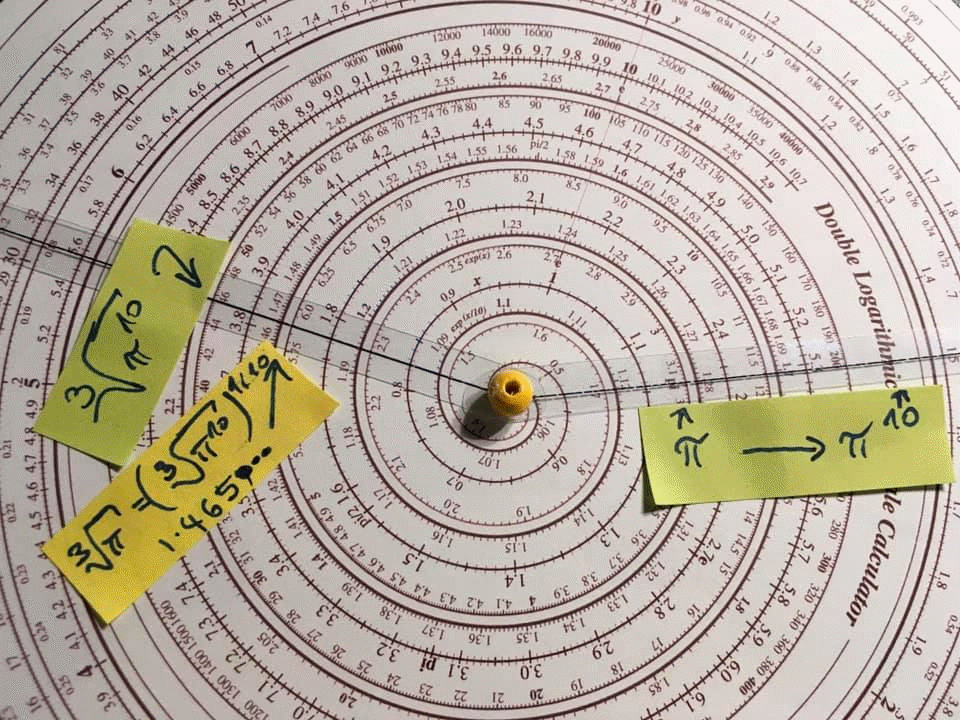
Obr. 5: Výpočet třetí odmocniny z π pomocí spirálového pravítka

Není bez zajímavosti, že použití několikrát obtočené stupnice („serpentiny“) na kruhovém pravítku vymyslel již jistý pan Milbourn z Yorkshiru kolem roku 1650. Přístroj pak skutečně vyrobil Thomas Brown, zmiňovaný jako výrobce matematických nástrojů (Maker of Mathematical Instruments). Podle dochovaného popisu se uspořádání stupnic pravítka skládalo z „Concentrick Circles“. [17] Nejednalo se tedy ve skutečnosti o spirálu, ale spíše o sérii kružnic, podobně jako u Fowlerova pravítka.

c) Pravděpodobnostní pravítko

Pravděpodobnostní pravítko (obr. 6) slouží k určení kvantilů vybraných rozdělení, konkrétně normálního rozdělení, Poissonova rozdělení (pro určení rizika selhání se známou očekávanou hodnotou) a Weibullova rozdělení, případně naopak k určení hodnoty distribuční funkce z daného kvantilu.

Všechna tato rozdělení závisí na charakteristikách, které do vzorce pro výpočet kvantilu vstupují jako součinitel, tj. se jimi násobí. Například u normálního rozdělení je touto charakteristikou známá směrodatná odchylka. Pomocí logaritmické stupnice lze tedy např. snadno vypočítat relativní polohu naměřené hodnoty vůči střední hodnotě (průměru). Této relativní poloze pak odpovídá výsledný kvantil (resp. percentil).

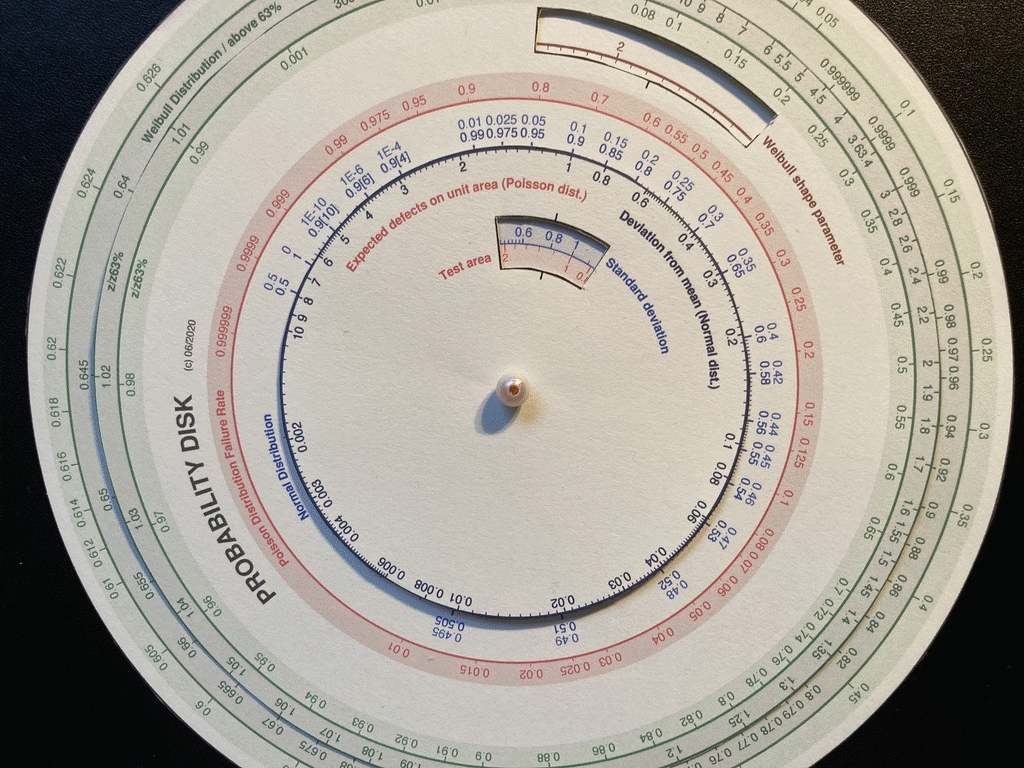
Obr. 6: Pravděpodobnostní pravítko

d) Hygrotermické pravítko

Ke speciálním účelům slouží též hygrotermické pravítko HYGROS hx (obr. 7). Zahrnuje všechny základní termodynamické vztahy mezi relativní vlhkostí, absolutní vlhkostí, teplotou a parciálním tlakem vlhkého vzduchu. Lze také vypočítat teplo (entalpii) potřebné například k ohřátí vzduchu na určitou teplotu. Podobná psychrometrická výpočetní pravítka se občas objevovala v průběhu 60. let 20. stol., nikoli však s takovým množstvím funkcí, jaké vidíte zde. Typickou úlohou z oblasti klimatizační techniky a stavební fyziky je určení rosného bodu, tj. teploty, při níž by za stávajících podmínek (při momentální teplotě a vlhkosti vzduchu) došlo ke kondenzaci vzdušné vlhkosti na mlhu. S tím souvisí i riziko vzniku plísní, které lze na površích v interiéru očekávat při 80% relativní vlhkosti.

Obr. 7: Hygrotermické pravítko HYGROS hx

Vzhledem ke složitějším vzájemným vztahům nejsou všechny stupnice logaritmické, ale částečně se řídí jinými zákony (např. teplotní stupnice). Z technického hlediska je zajímavé zejména použití několika okének, ve kterých lze odečíst např. hustotu vzduchu nebo podíl vody v celkovém objemu. Pro výpočet entalpie jsem navrhl izoentalpický nomogram, který používá vzdálenost od středu disku pro vynesení teploty, takže dokáže znázornit závislost entalpie zároveň na teplotě i na vlhkosti, tj. na dvou proměnných zároveň. Jednotlivé izočáry spojují body se stejnou entalpií. Na běžném, přímém logaritmickém pravítku by nic podobného nebylo možné.

e) Logické pravítko

Kruhová počítadla se dají použít nejen k numerickým výpočtům, ale také ke znázornění logických vztahů. Logické pravítko (obr. 8) jsem zkonstruoval jako poctu logikovi Augustu De Morganovi (1806–1871), [18] spoluzakladateli Londýnské matematické společnosti a příteli Charlese Babbage (1791–1871), vynálezce analytického stroje. De Morgan byl jedním ze zakladatelů predikátové logiky.

Obr. 8: Logické pravítko podle De Morgana

Na kotoučích jsou v zelených polích zobrazeny naproti sobě dvojice protichůdných výroků (subjektů X a predikátů Y) ve všech možných kombinacích. V šedých polích jsou tomu odpovídající formálně-logické zápisy tak, jak se používají pro vyjádření případů v teorii pravděpodobnosti.

f) Ars-Magna-Scheibe

A na závěr pohled do středověku. Pravítko „Ars Magna Nova" (obr. 9) je poctou „strojům na mylšení“ podle návrhů Ramóna Llulla. Kombinuje v sobě jeho nejznámější výtvory: pravítka „Ars Generalis Ultima“ a „Ars Brevis“ (1305–1308). Použitá terminologie je spíše novodobá a pravítko rozhodně neslouží k nalezení kosmické pravdy za pomoci mechanických kalkulací. Jednoduchým otázkám přiřazuje písmena, jak to zavedl Ramón Llull, a obměnou jejich kombinací vznikají sylogismy (přesně odpovídající otázkám Llullovy „Ars“), takže je lze použít k systematickému prozkoumání konkrétního problému.

Obr. 9. „Ars Magna Nova“ – stroj na myšlení podle Ramóna Llulla

3. Zhotovení pravítek

Základy

Při výrobě vlastních logaritmických pravítek je první otázkou jak vyrobit vzor pro tisk. Nejdůležitějšími kritérii jsou: čisté písmo, různé velikosti písma a možnosti grafické úpravy, možnost vyhotovit velké množství kopií a snadno provádět změny. Změny, opravy a nové nápady by neměly vést k nutnosti celý vzor překreslit znovu od začátku.

Z toho důvodu nejsou vhodné „statické“ postupy jako kreslení v grafickém editoru, PowerPointu a podobně. Hodí se nanejvýš ke zpracování koncepčních návrhů.

Mnohem lepší je rozmístění všech prvků na kotouči naprogramovat. Nejlépe tak, aby výsledkem byl obrázek ve vektorovém formátu, který lze snadno zvětšovat či zmenšovat, aniž by tím trpělo rozlišení. Velmi žádoucí je také vysoká míra flexibility v grafickém návrhu. Nechceme se omezit na jedno provedení grafického schématu s omezenou možností úprav, jako například v Excelu.

Jednou z výhod kruhových pravítek je to, že k jejich mechanickému seřízení není potřeba nic víc než přesné sesazení os otáčení (bez vůle). To samo o sobě stačí, aby i kotouče vyrobené např. z kartonu poskytovaly dostatečnou přesnost. Naproti tomu výroba klasického posuvného logaritmického pravítka s dostatečnou přesností je nepoměrně složitější. Ostatně dosti náročná je v takovém případě i samotná mechanická konstrukce pravítka. Nečekanou další výhodou je již výše zmíněná možnost zavést do čtení hodnot druhý rozměr a vedle úhlu natočení kotoučů použít jako proměnnou též vzdálenost od středu (viz pravítko HYGROS).

Programování

I když samozřejmě existuje mnoho jiných alternativ, já jsem se rozhodl použít Adobe Postscript. Tento grafický programovací jazyk je pro náš účel vhodný, protože vytváří vektorovou grafiku (formát Postscript), kterou lze následně převést i do formátu PDF (Portable Document Format), s nímž si většina programů dobře poradí. Postscript podporuje mnoho matematických operací a nejdůležitějších funkcí. Pomocí geometrických transformací lze části obrázků a textů zobrazit pod libovolným úhlem a v zásadě je k dispozici mnoho různých písem s měnitelnou velikostí.

Obr. 10 ukazuje část programu v Postscriptu, který generuje logaritmickou stupnici od 1 do 9. Největší specialitou Postscriptu je to, že při volání funkcí vč. těch nejjednodušších matematických operací pracuje se zásobníkem. Do něj se nejprve všechny parametry funkce vloží a při zavolání funkce se z něj čtou od posledního podle principu „Last in, first out“. Jako bychom odebírali uložené archeologické vrstvy shora dolů od nejnovější k nejstarší.

Obr. 10. Ukázka programu v postscriptu

Pohled do zdrojového kódu

Na řádku 11 .02 setlinewidth se nejprve do zásobníku vloží hodnota 0,02, která se potom přečte a použije při volání příkazu setlinewidth (zde pro nastavení šířky řádku). Definice úhlu natočení w pro výpočet souřadnic je následující: příkazem /w z log 360 mul def (řádek 4) se nejprve do zásobníku vloží nový identifikátor w, pak hodnota z; poté funkce log tuto hodnotu ze zásobníku přečte, spočítá logaritmus a výsledek vloží zpět do zásobníku. Následně se do zásobníku vloží číslo 360 a příkazem mul se obě naposledy vložené hodnoty (logaritmus z a 360) ze zásobníku přečtou, vynásobí a do zásobníku se vloží výsledek. Nakonec příkaz def tuto poslední hodnotu ze zásobníku přiřadí identifikátoru w. Výsledkem je, že jsme spočítali úhel w podle vzorce w = log(z) · 360. Takto zapsanému předpisu matematické funkce se také někdy říká „reverzní polská notace“ (RPN). Úhel, v němž rysky na pravítku vykreslujeme, se tedy postupně zvyšuje od 0 do 360 stupňů, ovšem s nerovnoměrným krokem, neboť proporce se mění podle toho, jak se mění proporce logaritmů čísel v jedné dekádě od 1 do 10.

Jednotlivé hodnoty se zpracovávají v cyklu for, jehož počáteční hodnotu, konečnou hodnotu a délku kroku jsme umístili do zásobníku hned v řádku 1. Po něm následuje sekvence příkazů ve složených závorkách (řádky 2 až 22), než se dojde k vlastnímu příkazu for. Složené závorky interpretu říkají, že kód uvnitř jimi ohraničeného bloku se nemá zpracovávat, ale celý umístit do zásobníku, kde jej pak příkaz for najde. Příkaz for tedy umístí řídící proměnnou (postupně od 1 do 9) do zásobníku. V řádku 3 se přidá identifikátor z a příkaz exch prohodí dvě hodnoty na vrchu zásobníku tak, že aktuální index for cyklu je nahoře a je přiřazen identifikátoru z. Ten se pak použije v řádku 4 pro výpočet úhlu, jak už je vysvětleno výše. Následující řádky provádějí podobné transformace pro další hodnoty potřebné k vykreslení stupnic. V řádcích 6 až 9 se počítají kartézské souřadnice pro rysky, které se mají nakreslit radiálně pod úhlem w, kde R je poloměr stupnice a sx označuje délku rysky. Ta se konečně nakreslí ve směru od středu ven příkazem lineto.

Zbývající úsek zdrojového kódu slouží k označení rysky číslicí, tj. hodnotou z, která se musí nejprve převést na řetězec s …

Pro složitější funkce se hodí předpočítat potřebné hodnoty i jejich popisky v Excelu, vyexportovat jako pole a vložit do připraveného postscriptového programu.

Tisk do PDF a montáž

Výsledek lze převést do souboru ve formátu PDF a vytisknout. Kvalita tiskárny by samozřejmě měla být co nejlepší. Chcete-li získat dostatečně pevný kotouč, tiskněte na silnější papír (160 g/m²). Potřebujete-li pravítko ještě odolnější, můžete výtisk podlepit i několika dalšími vrstvami papíru. Pro vystřižení či vyříznutí kotouče budete potřebovat jistou dávku zručnosti i přesnosti, zejména u pravítek s okénky. Běhoun se dá vyrobit z kousku fólie s vytištěnou černou linkou. Jednotlivé součástky se musí sestavit přesně soustředně a uprostřed spojit připínáčkem.

Pro další informace a výměnu zkušeností neváhejte kontaktovat autora na adrese sliderulesandmore@vodafonemail.de

Oliver Steffens, SLIDE RULES AND MORE

Prodej na eBay: https://www.ebay.de/sch/i.html?sid=sliderul_40

Z německého originálu „Rechenscheiben im 21. Jahrhundert: Revitalisierung einer historischen Rechentechnik“ přeložil Zdeněk Šustr, https://log.sustr.net; převzato s autorovým souhlasem

Reference